Simon Stevin (1548-1620)
The sixt Definition. A Whole number is either a unitie, or a compounded multitude of unities.
Simon Stevin, sometimes called Stevinus, was a Flemish mathematician, physicist and military engineer. He made various contributions in many areas of science and engineering, both theoretical and practical. He also translated various mathematical terms into Dutch, making it one of the few European languages in which the word for mathematics, wiskunde wis and kunde, i.e., "the knowledge of what is certain", was not a loanword from Greek but a calque via Latin. He also replaced the word chemie, the Dutch for chemistry, by scheikunde "the art of separating", made in analogy with wiskunde.
Biography
Very little is known with certainty about Stevin's life and what we know is mostly inferred from other recorded facts. The exact birth date and the date and place of his death are uncertain. It is assumed he was born in Bruges since he enrolled at Leiden University under the name Simon Stevinus Brugensis meaning "Simon Stevin from Bruges". His name is usually written as Stevin, but some documents regarding his father use the spelling Stevijn pronunciation . This is a normal spelling shift in 16th-century Dutch. Simon's mother, Cathelijne or Catelyne was the daughter of a wealthy family from Ypres. Her father Hubert was a poorter of Bruges. Cathelijne later married Joost Sayon who was involved in the carpet and silk trade and a member of the schuttersgilde Sint-Sebastiaan. Through her marriage Cathelijne became a member of a family of Calvinists and Simon was likely brought up in the Calvinist faith.
It is believed that Stevin grew up in a relatively affluent environment and enjoyed a good education. He was likely educated at a Latin school in his hometown.
Simon Stevin's travels
Stevin left Bruges in 1571 apparently without a particular destination. Stevin was most likely a Calvinist since a Catholic would likely not have risen to the position of trust he later occupied with Maurice, Prince of Orange. It is assumed that he left Bruges to escape the religious persecution of Protestants by the Spanish rulers. Based on references in his work "Wisconstighe Ghedaechtenissen" Mathematical Memoirs, it has been inferred that he must have moved first to Antwerp where he began his career as a merchant's clerk. Some biographers mention that he travelled to Prussia, Poland, Denmark, Norway and Sweden and other parts of Northern Europe, between 1571 and 1577. It is possible that he completed these travels over a longer period of time. In 1577 Simon Stevin returned to Bruges and was appointed city clerk by the aldermen of Bruges, a function he occupied from 1577–1581. He worked in the office of Jan de Brune of the Brugse Vrije, the castellany of Bruges.
Why he had returned to Bruges in 1577 is not clear. It may have been related to the political events of that period. Bruges was the scene of intense religious conflict. Catholics and Calvinists alternately controlled the government of the city. They usually opposed each other but would occasionally collaborate in order to counteract the dictates of King Philip II of Spain. In 1576 a certain level of official religious tolerance was decreed. This could explain why Stevin returned to Bruges in 1577. Later the Calvinists seized power in many Flemish cities and incarcerated Catholic clerics and secular governors supportive of the Spanish rulers. Between 1578 and 1584 Bruges was ruled by Calvinists.
Simon Stevin in the Netherlands
In 1581 Stevin left his native Bruges and moved to Leiden where he attended the Latin school. On 16 February 1583 he enrolled, under the name Simon Stevinus Brugensis meaning "Simon Stevin from Bruges", at Leiden University, which had been founded by William the Silent in 1575. Here he befriended William the Silent's second son and heir Prince Maurice, the Count of Nassau. Stevin is listed in the University's registers until 1590 and apparently never graduated.

Following William the Silent's assassination and Prince Maurice's assumption of his father's office, Stevin became the principal advisor and tutor of Prince Maurice. Prince Maurice asked his advice on many occasions, and made him a public officer – at first director of the so-called "waterstaet" the government authority for public works, especially water management from 1592, and later quartermaster-general of the army of the States-General. Prince Maurice also asked Stevin to found an engineering school within the University of Leiden.
Stevin moved to The Hague where he bought a house in 1612. He married in 1610 or 1614 and had four children. It is known that he left a widow with two children at his death in Leiden or The Hague in 1620.
- Statue of Simon Stevin by Eugène Simonis, on the Simon Stevinplein [nl] in Bruges
- Statue of Stevin detail
- Statue detail: Inclined plane diagram
- Statue detail showing experiments on hydrostatic equilibrium
Discoveries and inventions
Stevin is responsible for many discoveries and inventions. He was a pioneer of the development and the practical application of engineering related science such as mathematics, physics and applied science like hydraulic engineering and surveying. He was thought to have invented the decimal fractions until the middle of the 20th century, but researchers later discovered that decimal fractions were already introduced by the medieval Islamic scholar al-Uqlidisi in a book written in 952. Moreover, a systematic development of decimal fractions was given well before Stevin in the book Miftah al-Hisab written in 1427 by Al-Kashi.

His contemporaries were most struck by his invention of a so-called land yacht, a carriage with sails, of which a model was preserved in Scheveningen until 1802. The carriage itself had been lost long before. Around the year 1600 Stevin, with Prince Maurice of Orange and twenty-six others, used the carriage on the beach between Scheveningen and Petten. The carriage was propelled solely by the force of wind and acquired a speed which exceeded that of horses.
Management of waterways
Stevin's work in the waterstaet involved improvements to the sluices and spillways to control flooding, exercises in hydraulic engineering. Windmills were already in use to pump the water out but in Van de Molens On mills, he suggested improvements including ideas that the wheels should move slowly with a better system for meshing of the gear teeth. These improved threefold the efficiency of the windmills used in pumping water out of the polders. He received a patent on his innovation in 1586.
Philosophy of science
Stevin's aim was to bring about a second age of wisdom, in which mankind would have recovered all of its earlier knowledge. He deduced that the language spoken in this age would have had to be Dutch, because, as he showed empirically, in that language, more concepts could be indicated with monosyllabic words than in any of the European languages he had compared it with. This was one of the reasons why he wrote all of his works in Dutch and left the translation of them for others to do. The other reason was that he wanted his works to be practically useful to people who had not mastered the common scientific language of the time, Latin. Thanks to Simon Stevin the Dutch language got its proper scientific vocabulary such as "wiskunde" "kunst van het gewisse of zekere" the art of what is known or what is certain for mathematics, "natuurkunde" the "art of nature" for physics, "scheikunde" the "art of separation" for chemistry, "sterrenkunde" the "art of stars" for astronomy, "meetkunde" the "art of measuring" for geometry.
Geometry, physics and trigonometry
Stevin was the first to show how to model regular and semiregular polyhedra by delineating their frames in a plane. He also distinguished stable from unstable equilibria.
Stevin contributed to trigonometry with his book, De Driehouckhandel.
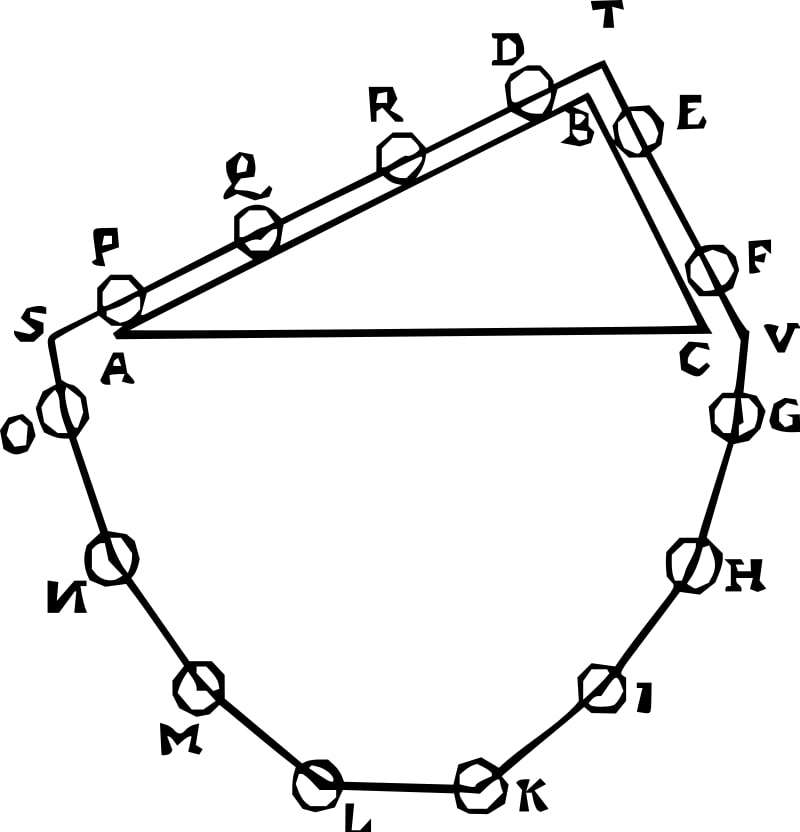
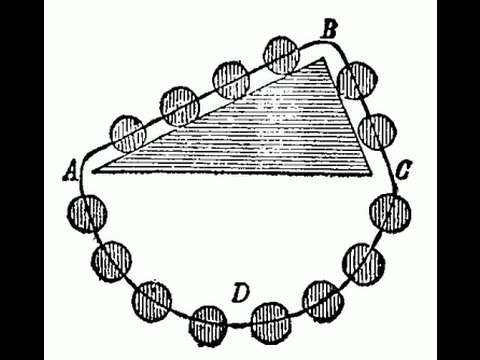
In THE FIRST BOOK OF THE ELEMENTS OF THE ART OF WEIGHING, The second part: Of the propositions , Page 41, Theorem XI, Proposition XIX, he derived the condition for the balance of forces on inclined planes using a diagram with a "wreath" containing evenly spaced round masses resting on the planes of a triangular prism see the illustration on the side. He concluded that the weights required were proportional to the lengths of the sides on which they rested assuming the third side was horizontal and that the effect of a weight was reduced in a similar manner. It's implicit that the reduction factor is the height of the triangle divided by the side the sine of the angle of the side with respect to the horizontal. The proof diagram of this concept is known as the "Epitaph of Stevinus". As noted by E. J. Dijksterhuis, Stevin's proof of the equilibrium on an inclined plane can be faulted for using perpetual motion to imply a reductio ad absurdum. Dijksterhuis says Stevin "intuitively made use of the principle of conservation of energy ... long before it was formulated explicitly.":54

He demonstrated the resolution of forces before Pierre Varignon, which had not been remarked previously, even though it is a simple consequence of the law of their composition.
Stevin discovered the hydrostatic paradox, which states that the pressure in a liquid is independent of the shape of the vessel and the area of the base, but depends solely on its height.
He also gave the measure for the pressure on any given portion of the side of a vessel.
He was the first to explain the tides using the attraction of the moon.
In 1586, he demonstrated that two objects of different weight fall with the same acceleration.
Music theory
The first mention of equal temperament related to the twelfth root of two in the West appeared in Simon Stevin's unfinished manuscript Van de Spiegheling der singconst ca 1605 published posthumously three hundred years later in 1884; however, due to insufficient accuracy of his calculation, many of the numbers for string length he obtained were off by one or two units from the correct values. He appears to have been inspired by the writings of the Italian lutenist and musical theorist Vincenzo Galilei father of Galileo Galilei, a onetime pupil of Gioseffo Zarlino.
Bookkeeping
Bookkeeping by double entry may have been known to Stevin, as he was a clerk in Antwerp in his younger years, either practically or through the medium of the works of Italian authors such as Luca Pacioli and Gerolamo Cardano. However, Stevin was the first to recommend the use of impersonal accounts in the national household. He brought it into practice for Prince Maurice, and recommended it to the French statesman Sully.
Decimal fractions
Stevin wrote a 35-page booklet called De Thiende "the art of tenths", first published in Dutch in 1585 and translated into French as La Disme. The full title of the English translation was Decimal arithmetic: Teaching how to perform all computations whatsoever by whole numbers without fractions, by the four principles of common arithmetic: namely, addition, subtraction, multiplication, and division. The concepts referred to in the booklet included unit fractions and Egyptian fractions. Muslim mathematicians were the first to utilize decimals instead of fractions on a large scale. Al-Kashi's book, Key to Arithmetic, was written at the beginning of the 15th century and was the stimulus for the systematic application of decimals to whole numbers and fractions thereof. But nobody established their daily use before Stevin. He felt that this innovation was so significant, that he declared the universal introduction of decimal coinage, measures and weights to be merely a question of time.

His notation is rather unwieldy. The point separating the integers from the decimal fractions seems to be the invention of Bartholomaeus Pitiscus, in whose trigonometrical tables 1612 it occurs and it was accepted by John Napier in his logarithmic papers 1614 and 1619.
Stevin printed little circles around the exponents of the different powers of one-tenth. That Stevin intended these encircled numerals to denote mere exponents is clear from the fact that he employed the very same symbol for powers of algebraic quantities. He did not avoid fractional exponents; only negative exponents do not appear in his work.
Stevin wrote on other scientific subjects – for instance optics, geography, astronomy – and a number of his writings were translated into Latin by W. Snellius Willebrord Snell. There are two complete editions in French of his works, both printed in Leiden, one in 1608, the other in 1634.
Mathematics
Stevin wrote his Arithmetic in 1594. The work brought to the western world for the first time a general solution of the quadratic equation, originally documented nearly a millennium previously by Brahmagupta in India.
According to van der Waerden, Stevin eliminated "the classical restriction of 'numbers' to integers Euclid or to rational fractions Diophantos...the real numbers formed a continuum. His general notion of a real number was accepted, tacitly or explicitly, by all later scientists". A recent study attributes a greater role to Stevin in developing the real numbers than has been acknowledged by Weierstrass's followers. Stevin proved the intermediate value theorem for polynomials, anticipating Cauchy's proof thereof. Stevin uses a divide and conquer procedure subdividing the interval into ten equal parts. Stevin's decimals were the inspiration for Isaac Newton's work on infinite series.
Neologisms
Stevin thought the Dutch language to be excellent for scientific writing, and he translated many of the mathematical terms to Dutch. As a result, Dutch is one of the few Western European languages that have many mathematical terms that do not stem from Greek or Latin. This includes the very name Wiskunde Mathematics.
His eye for the importance of having the scientific language be the same as the language of the craftsman may show from the dedication of his book De Thiende 'The Disme' or 'The Tenth': 'Simon Stevin wishes the stargazers, surveyors, carpet measurers, body measurers in general, coin measurers and tradespeople good luck.' Further on in the same pamphlet, he writes: " teaches us all calculations that are needed by the people without using fractions. One can reduce all operations to adding, subtracting, multiplying and dividing with integers."

Some of the words he invented evolved: 'aftrekken' subtract and 'delen' divide stayed the same, but over time 'menigvuldigen' became 'vermenigvuldigen' multiply, the added 'ver' emphasizes the fact it is an action. 'Vergaderen' became 'optellen' add.
Another example is the Dutch word for diameter: 'middellijn', lit.: line through the middle.
The word 'zomenigmaal' quotient lit. 'that many times' has become the perhaps less poetic 'quotiënt' in modern-day Dutch.
Other terms did not make it into modern day mathematical Dutch, like 'teerling' die, although still being used in the meaning as die, instead of cube. His books were bestsellers.
Trivia
The study association of mechanical engineering at the Technische Universiteit Eindhoven, W.S.V. Simon Stevin, is named after Simon Stevin. In Stevin's memory, the association calls its bar "De Weeghconst" and owns a self-built fleet of land yachts.
Stevin, cited as Stevinus, is one of the favorite authors – if not the favorite author – of Uncle Toby Shandy in Laurence Sterne's The Life and Opinions of Tristram Shandy Gentleman.
Quote: A man in anger is no clever dissembler.

In Bruges there is a Simon Stevin Square which holds a statue of Stevin made by Eugène Simonis. The statue incorporates Stevin's inclined plane diagram.
Operating from the port of Oostende is a research/survey vessel named after him.
Publications
Amongst others, he published:
- Tafelen van Interest Tables of interest in 1582 with present value problems of simple and compound interest and interest tables that had previously been unpublished by bankers;
- Problemata geometrica in 1583;
- De Thiende La Disme, The tenth in 1585 in which decimals were introduced in Europe;
- La pratique d'arithmétique in 1585;
- L'arithmétique in 1585 in which he presented a uniform treatment for solving algebraic equations;
- Dialectike ofte bewysconst Dialectics, or Art of Demonstration in 1585 at Leyden by Christoffel Plantijn. Published again in 1621 at Rotterdam by Jan van Waesberge de Jonge.
- De Beghinselen Der Weeghconst in 1586, accompanied by De Weeghdaet;
- De Beghinselen des Waterwichts Principles on the weight of water in 1586 on the subject of hydrostatics;
- Vita Politica. Named Burgherlick leven Civil life in 1590;
- De Stercktenbouwing The construction of fortifications published in 1594;
- De Havenvinding Position finding published in 1599;
- De Hemelloop in 1608 in which he voiced support for the Copernican theory.
- In Wiskonstighe Ghedachtenissen Mathematical Memoirs, Latin: Hypomnemata Mathematica from 1605 to 1608. This included Simon Stevin's earlier works like De Driehouckhandel Trigonometry, De Meetdaet Practice of measuring, and De Deursichtighe Perspective, which he edited and published.;
- Castrametatio, dat is legermeting and Nieuwe Maniere van Stercktebou door Spilsluysen New ways of building of sluices published in 1617;
- De Spiegheling der Singconst Theory of the art of singing.
- "Œuvres mathématiques..., Leiden, 1634